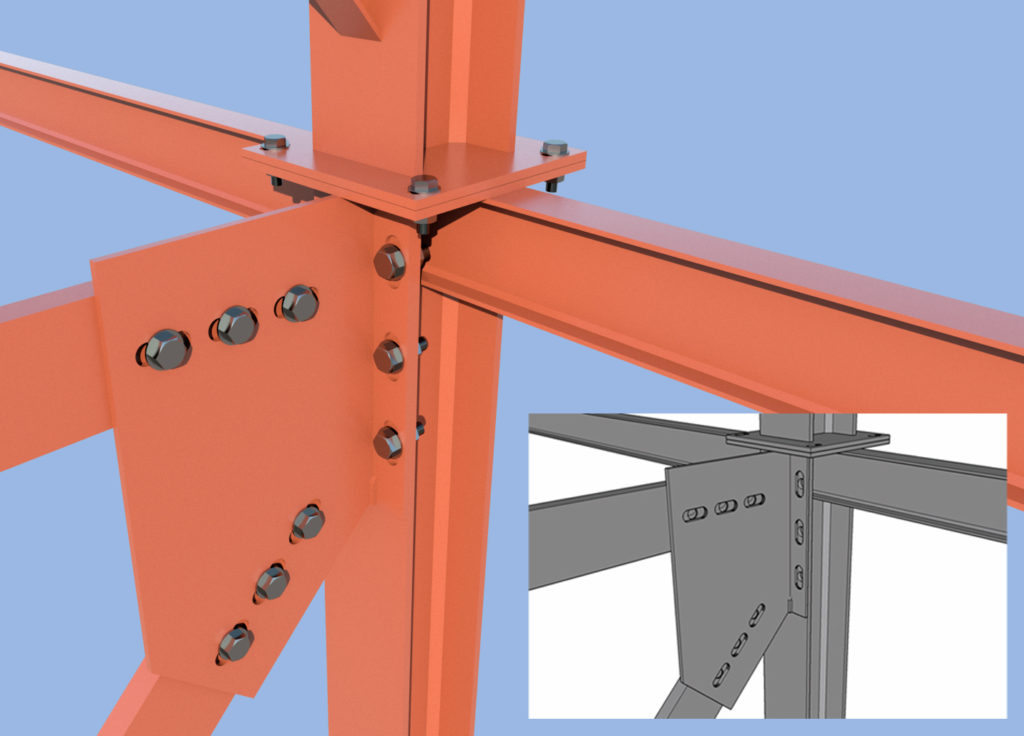
Em estruturas de aço, é comum a utilização de ligações aparafusadas com furos ranhurados (furos passantes) para permitir a expansão livre dos elementos sob cargas térmicas. É interessante analisar como este comportamento pode ser modelado numa estrutura como um todo em termos de expansão livre(e).
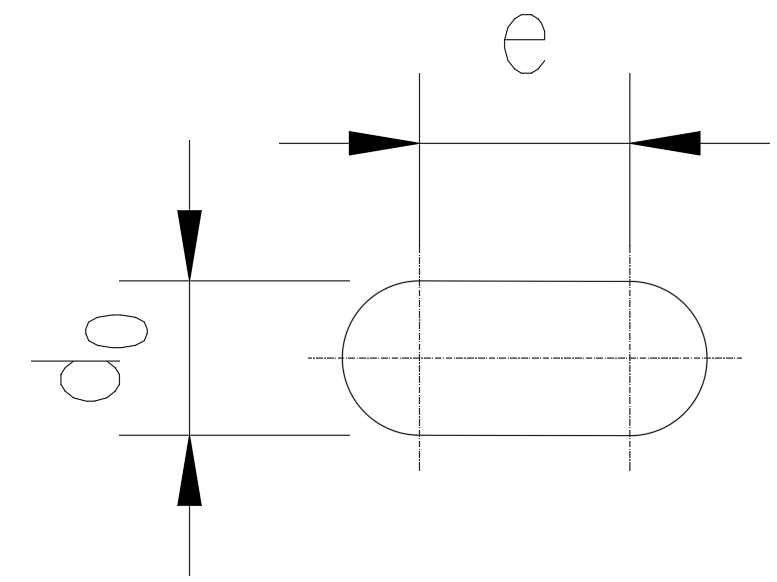
Figura 1 – Furo rasgado de diâmetro d0 e comprimento livre e.
O processo de conceção natural deve ser o seguinte:
- Calcula o deslocamento máximo de dilatação da estrutura que afectaria a junta em questão.
- Com base no cálculo acima, determina o comprimento e suficiente para permitir a livre expansão.
Se for esse o caso, já se sabe que o elemento em questão pode expandir-se livremente e a modelação deste comportamento envolve apenas a libertação da restrição ao deslocamento longitudinal (aplicação de uma libertação). Conceptualmente, a modelação de uma viga biaxialmente apoiada sujeita a uma temperatura uniforme seria a seguinte:
Figura 2 – Modelação concetual de uma viga de duas pernas com expansão livre permitida numa das extremidades.
No entanto, é comum que as caraterísticas das juntas aparafusadas sejam impostas por normas, o que pode fazer com que a dimensão e seja insuficiente. Ou seja, pode acontecer que a barra tente expandir-se mais do que a rotura da junta lhe permite. Neste caso, o comportamento do apoio de expansão livre tem dois modos:
- Expansão livre desde que o deslocamento longitudinal (u1) seja inferior a e.
- Restrição de deslocamento longitudinal (e consequente ocorrência de tensões de compressão) quando u1=e.
O esquema concetual seria o seguinte:
Figura 3 – Modelação concetual de uma viga de duas pernas com deslocamento longitudinal parcialmente permitido num dos apoios.
Vejamos um exemplo:
Uma barra bipolar é sujeita a um aumento de temperatura de 72 0Cacima da temperatura de instalação(300 devido à temperatura ambiente e420 devido à radiação solar). A barra tem um perfil IPE220, é feita de aço S275 e o seu comprimento total é de 20m. Numa das extremidades, o suporte permite um deslocamento de 1 cm.
A expansão longitudinal de uma barra, no caso de não haver restrições, é calculada como
ΔL=αL-ΔT-L
Ser:
ΔL: alongamento a uma temperatura uniforme.
αL: Coeficiente de expansão linear do material.
ΔT: Aumento da temperatura.
L: Comprimento inicial da barra.
Obtém o seguinte resultado:
|
L (m) |
20 |
|
aL (0C-1) |
1.20E-05 |
|
DT(0C) |
72 |
|
DL (cm) |
1.73 |
Tabela 1 – Deflexão de expansão livre.
Como a deformação permitida pelo suporte é de 1 cm, a barra sofrerá dois processos:
- Expande-se livremente até ter alongado 1 cm sem esforço.
- Deixa de se expandir e sofre o esforço de compressão axial correspondente à tentativa de expansão dos 0,73 cm que o suporte não permite.
A tensão produzida é o equivalente à tensão na barra quando esta é encurtada em 0,73 cm.
É fácil obter esta força axial através da teoria clássica da força:
|
L (m) |
20 |
Perfil |
IPE220 |
|
|
aL (0C-1) |
1.20E-05 |
A (cm2) |
33.4 |
|
|
DL (cm) |
-0.73 |
E (MPa) |
210,000 |
|
|
|
|
e |
3.64E-04 |
|
|
|
|
N (kN) |
-255.31 |
|
|
s (MPa) |
-76.44 |
|||
|
fy (MPa) |
275 |
|||
|
s / fy |
27.80% |
Tabela 2 – Cálculo da força axial produzida quando a barra se expandiu tanto quanto o suporte permite.
As tensões causadas pela restrição aplicada correspondem a quase 30% da tensão de cedência e, por conseguinte, não são de modo algum negligenciáveis.
O que este exemplo simples demonstra é que seriam cometidos erros de cálculo significativos se esta estrutura fosse modelada com um deslocamento longitudinal livre numa extremidade ou com um deslocamento longitudinal restringido em ambos os apoios.
Trata-se de um comportamento não linear (como tem duas fases diferentes, o comportamento perde a linearidade) que é simples de entender e calcular em casos tão simples como o aqui descrito, mas que em muitas situações coloca um problema para a sua modelação em programas de cálculo estrutural.
Então, como é que o modelamos num programa de cálculo?
A forma de resolver este tipo de problema é normalmente utilizar um elemento de folga e efetuar uma análise não linear. O esquema concetual deste elemento é o seguinte:
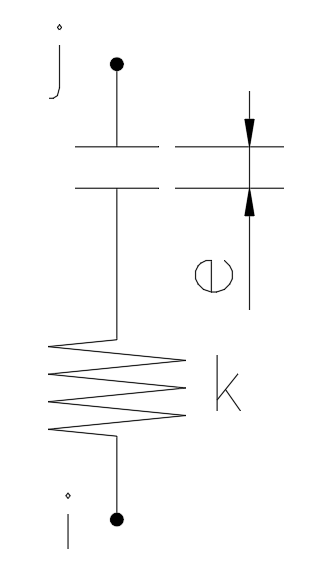
Figura 4 – Diagrama concetual de um elemento de lacuna.
O rácio de força (f) – deformação (def) deste elemento numa direção é dada por
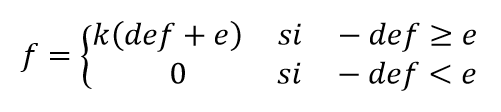
Ser def negativo se for um encurtamento.
Este elemento tem muitas aplicações e é útil numa série de casos práticos. Para o caso que estamos a tratar aqui, o parâmetro e corresponde ao comprimento de deformação livre que existe na junta, enquanto a rigidez pode ser tomada como infinita (algumas ordens de grandeza acima da rigidez da estrutura). Por outras palavras, com esta configuração, permitiríamos que os nós i e j se aproximassem um do outro até que o espaço fosse fechado. A partir desse ponto, não permite mais encurtamentos.
No software SAP2000, o elemento gap está incluído nos elementos de tipo de ligação. Assim, ao definir as caraterísticas de uma ligação, é possível configurá-la para atuar conforme explicado acima.
Segue-se um esboço do processo de criação de uma ligação de lacunas para modelar o exemplo acima referido.
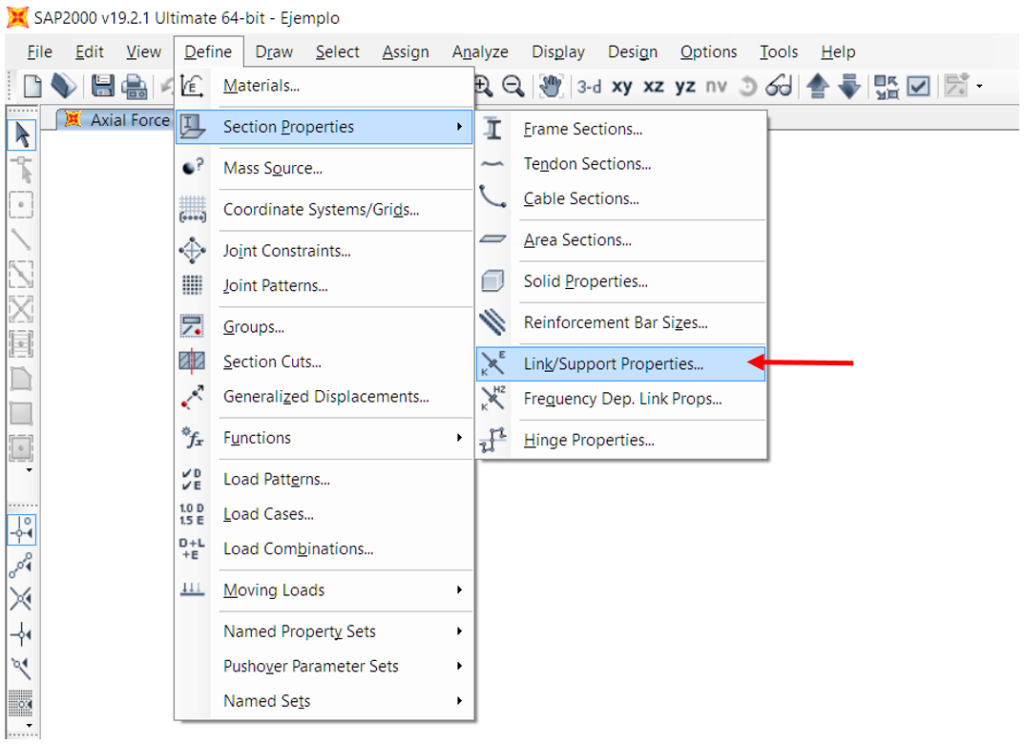
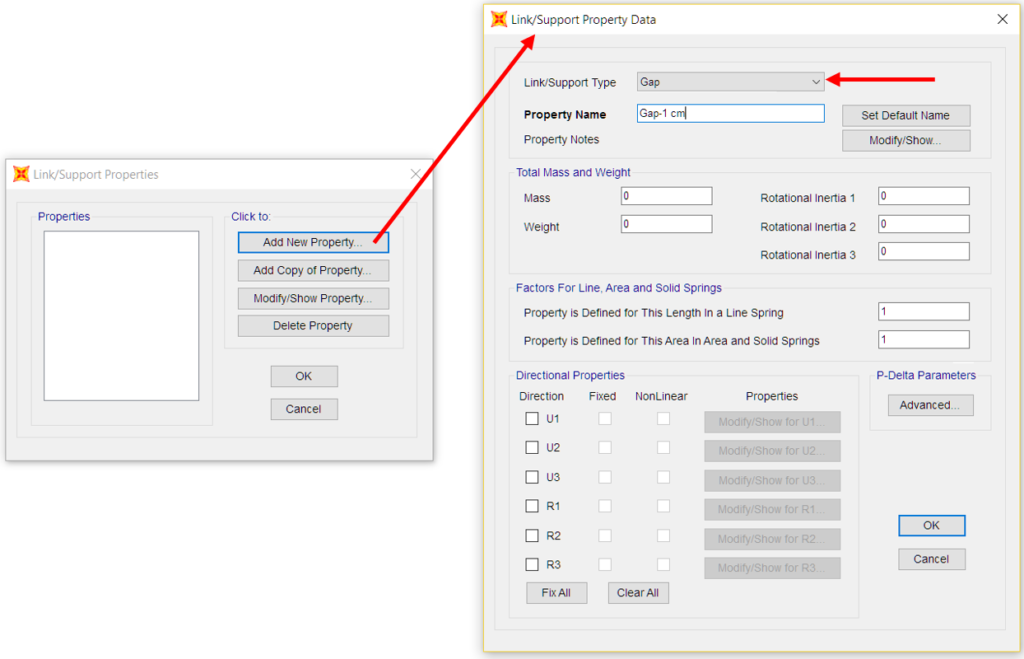
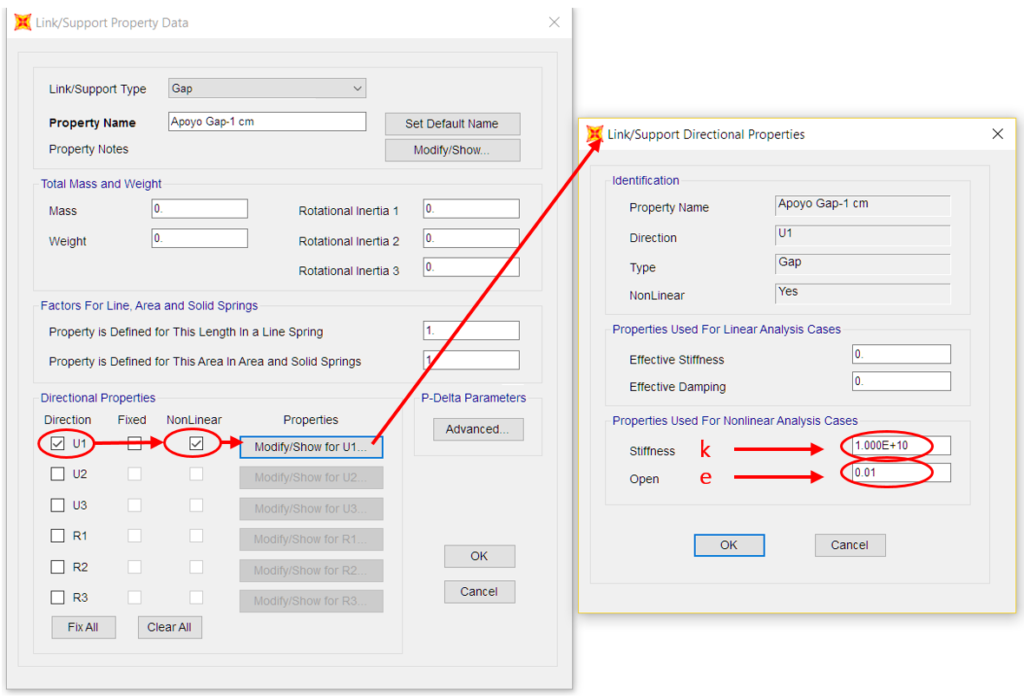Figura 5 – Processo de configuração de um elemento de gap no SAP2000.
Para definir uma rigidez que não permita deslocamentos para além do comprimento e, não se recomenda a utilização de um valor exageradamente elevado, mas sim um valor entre 1 e 3 ordens de grandeza superior à rigidez dos elementos vizinhos. Valores demasiado elevados podem levar à geração de matrizes singulares.
Uma vez definido o elemento, a geometria e as ligações externas do problema anterior podem ser configuradas da seguinte forma:
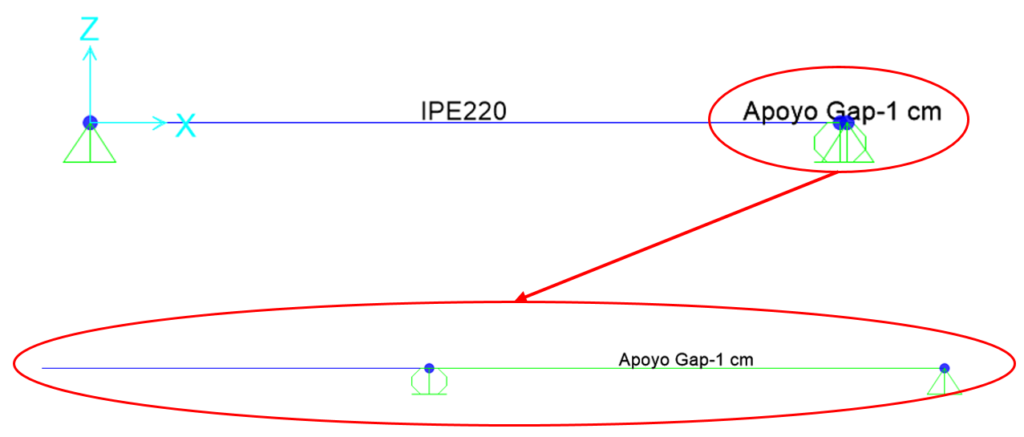Figura 6 – Configuração do apoio com elemento de folga na direção longitudinal.
Esta configuração é apenas uma das configurações possíveis. Como se pode observar, o deslocamento longitudinal no apoio real foi libertado, tendo sido criado outro apoio fictício no exterior da estrutura. Entre estes dois apoios, é colocado o elemento de folga (ligação de 2 articulações), que apenas permitirá um deslocamento de 1 cm na direção X no apoio real.
Uma vez criada a configuração geométrica, os valores de temperatura720 são aplicados ao barramento e o caso de carga afetado é configurado como NÃO-LINEAR. Nos casos de carga que não estejam definidos como NÃO-LINEARES, esta ligação não terá qualquer repercussão.
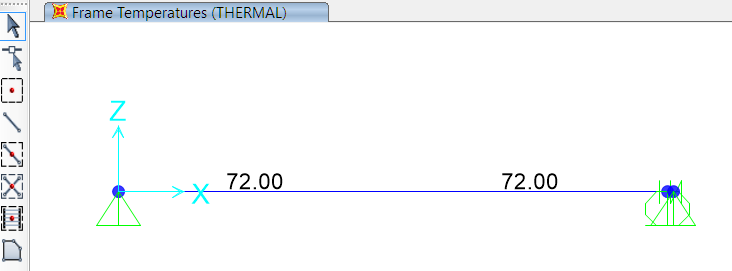Figura 7 – Temperatura aplicada à barra.
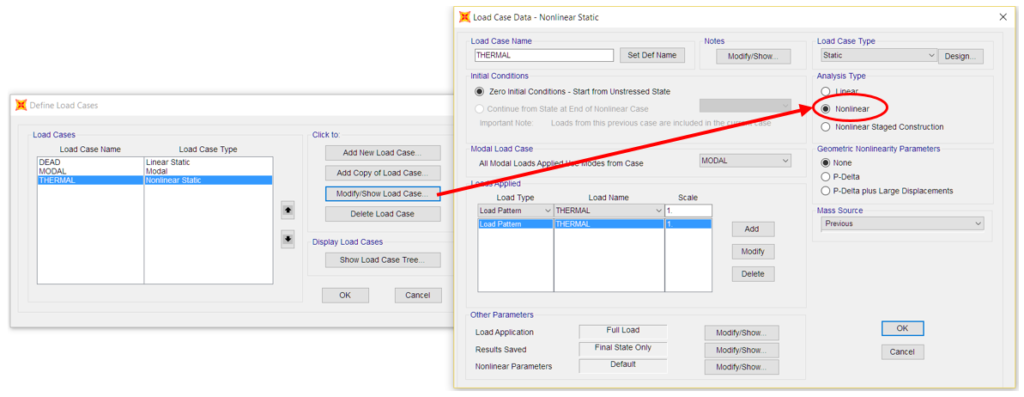Figura 8 – Configuração dos casos de carga como NÃO-LINEARES.
Uma vez implementada esta configuração e efectuados os cálculos, os resultados obtidos em termos de tensões e deformações são os mesmos que os calculados anteriormente:
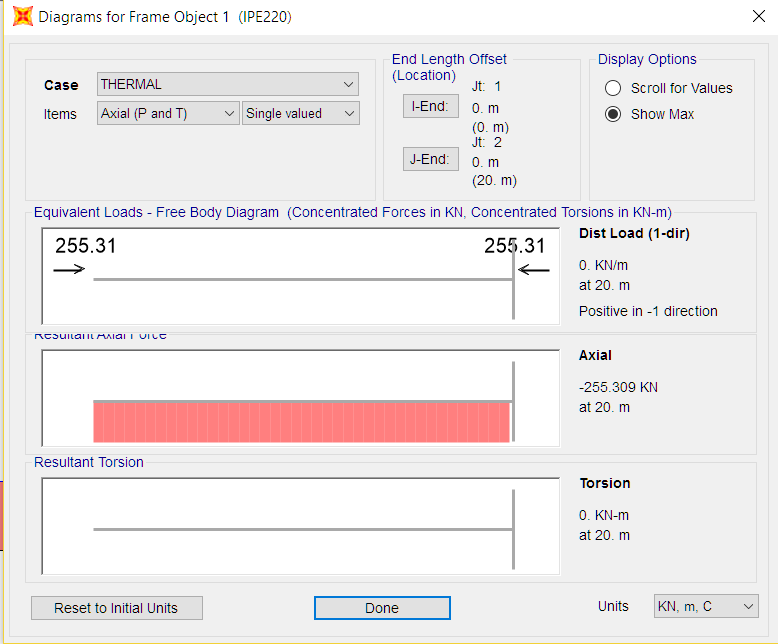
Figura 9 – Diagrama de tensões da barra (força axial de -255,31 kN).
Figura 10 – Deslocamentos em apoio extremo (1 cm).
Este é talvez o caso mais simples de aplicação do elemento de folga, no entanto, é suficientemente ilustrativo para mostrar as possibilidades do elemento. Através da definição da ligação, podemos implementar o comportamento de uma abertura independente em cada grau de liberdade, ou fixar todos os movimentos no l.d.g. que nos interessa, etc. Assim, pode ser muito útil sempre que exista um intervalo que consideremos importante tratar na nossa estrutura.
Por exemplo, na figura seguinte, foi utilizado para modelar o espaço entre duas partes de uma plataforma assente no mesmo pilar. Neste caso particular, se não for incluída a ligação do tipo gap, cada plataforma desloca-se longitudinalmente sem ter em conta a “colisão” com a adjacente. Na configuração deste elemento, foram fixados os deslocamentos verticais e transversais das plataformas, de acordo com as caraterísticas dos apoios reais.
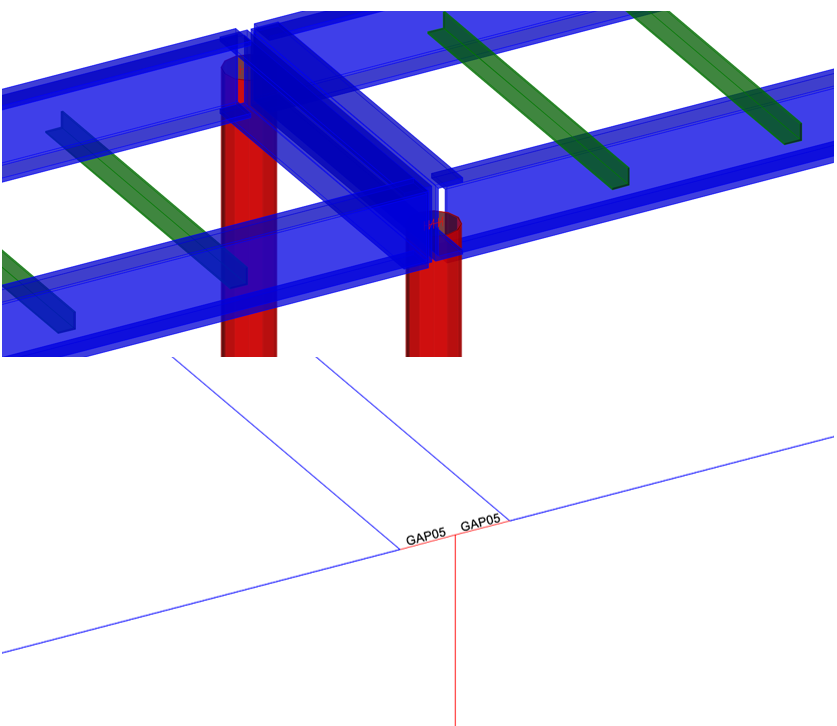
Figura 11 – Exemplo de utilização de elementos de folga.
Podes encontrar mais exemplos interessantes na seguinte ligação (neste caso, para ter em conta edifícios adjacentes, mas ligeiramente separados, que podem influenciar o cálculo dinâmico).
Existe também um elemento para modelar o oposto, as aberturas que podem ser abertas até um determinado comprimento, os elementos de gancho.
Espero que este post seja útil e vejo-te em breve!
